This topic is very different than many of my previous topics. It is about math!! First I am not a mathematician and not a big fan of fan. It is hard.
The story started here when I saw this video. I love this channel and I have watched most of its video.
First let's mention the rule here, take any positive integer number:
if number is odd then multiply it by 3 and add 1.
N−>3N+1
if number is even then divide it by two.
We can deduce a sequence here:
A digit ends with 1 will always gives a digit ends with 4. because
For even numbers; we can deduce them using the following tables:
Now we have all the information we need to draw a state machine diagram for these numbers:
you can verify this with any number generated by the 3N+1 problem and the sequence will always be valid.
What can we see in this graph:
1- The blue lines are where we divide by 2 hence reduce the value. The red lines are where we multiply by 3 and add 1 hence increase the value.
2- Blue lines are 10 and red lines are only 5. That means overall the value should decrease even if it is increased for sometime.
4- Loops {6,3,0,5,6,...} can never be broken except at number 6 only. Loops {9,8,9,8...} can be broken at number 8 only. Loops can only be broken at even numbers only.
5- Loop {1,4,2,1,4,2,....} there are two blue lines and one red line. The result is 1 when n =1 that is why it loops forever.
The number will either loop in Zero or get out in 6 to 8 because incrementing by 10/4 is 2.5
Similar rules is applied to {8,9} and {4,7,2,1} loops. remember only balanced loop is {4,2,1} when n is {4,2,1}.
7- If you get out of a loop then to get in again you pass one or more blue lines. if you are in loop 6 and move to loop 8 and come back to 6 using worst path you need to move on {6, 8, 9, 4, 7, 2, 6} which is 2 red lines and five blue lines. The number is ALWAYS reduce.
So you have thre main rules guide the behavior here.
A- You cannot loop in one loop forever except {4,2,1}.
B- Jumping from one loop to another reduces the value.
C- Moving back and forth from loop 6 to loop 8 requires passing on loop 4. It is a Must.
So as value gets smaller and passes via 4 from 8 that explains the 4 ,2 ,1.
I know this is NOT a scientific mathematical proof. But it explains to certain extend the behavior of this formula.

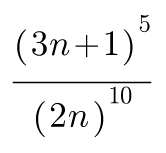
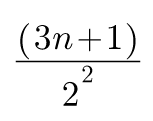
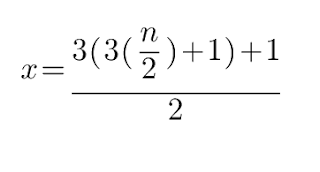

No comments:
Post a Comment